 |
|
|---|
 |
|
|---|
 |
|---|
| CONTENTS |
|
|
Rapid cooling and solidification during melt spinning and strip casting result from highly effective heat transfer at the interface between the ribbon and the spinning wheel. In order to control the free-surface stability and enhance the interface heat transfer, it is effective to apply a uniform force on the ribbon after the liquid melt impinges onto the spinning wheel. This article employs finite-element analysis with the assumption of two-dimensional eddy currents in the melt-spun ribbon to solve the current vector potential and eddy-current density governing equations. The distributions of eddy current and Lorentz force on the moving ribbon at a speed of 0-50 m/s are discussed; the effects of coil diameter and coil current on the Lorentz force's distribution are also considered. This investigation suggests a possible way to improve the single- and twin-roll casting technology in industry.
| Table I. Process Parameters and Material Properties in a Typical PFC Process | |
|---|---|
| Process Parameters | |
| Gap (G) | 10-3 m |
| Slot (S) | 10-3 m |
| Overpressure (P) | 2 x 103Pa |
| Wheel Speed (U) | 10 m/s |
| Wheel Radius (Rw) | 1 m |
| Puddle Length (L) | 10-2 m |
| Ribbon Thickness (T) | 10-4 m |
Solidification Time ( s) s) |
10-3 s |
| Properties | |
Density ( ) ) |
2,300Kg/m3 |
| Viscosity (v) | 10-3 N-s/m2 |
Surface Tension (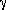 ) ) |
0.85 N/m |
| Resulting Dimensionless Parameters | |
| S/G = 1 | |
| T/G = 10-1 | |
| T/L = 10-2 | |
| Reynolds Number (Re) |  UG/µ = 23,000 UG/µ = 23,000  104 104 |
| Weber Number (We) |  U2/(2 U2/(2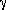 /G) = 135 /G) = 135  102 102 |
| No Name (Pbar) | P/(2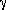 /G) = 1.18 /G) = 1.18  1 1 |
 1 m/s), while planar-flow melt spinning is preferred in ribbon production at high wheel speed (>1 m/s). Praisner et al.3 conducted an experimental study to determine process behavior in PFC. Flow stability during solidification was illustrated by Steen and Karcher,4 and numerical modeling of solidification heat transfer in spin-casting was given by Chen et al.5 A heat-transfer analysis weakly coupled to fluid flow was performed to give insight into the solidification front and melt undercooling.6 Process and microstructure evaluations in the melt spinning of Ti-Al are given in Reference 7. Interfacial heat transfer of metal casting on a moving substrate is reported in Reference 8.
1 m/s), while planar-flow melt spinning is preferred in ribbon production at high wheel speed (>1 m/s). Praisner et al.3 conducted an experimental study to determine process behavior in PFC. Flow stability during solidification was illustrated by Steen and Karcher,4 and numerical modeling of solidification heat transfer in spin-casting was given by Chen et al.5 A heat-transfer analysis weakly coupled to fluid flow was performed to give insight into the solidification front and melt undercooling.6 Process and microstructure evaluations in the melt spinning of Ti-Al are given in Reference 7. Interfacial heat transfer of metal casting on a moving substrate is reported in Reference 8.
Despite these research efforts, two major issues still exist in PFC: in single-roll casting or melt spinning, the instability of the free surface and meniscus often causes rough or rippled ribbon surfaces, and once solidification begins, heat transfer is reduced due to the poor solid-solid (solidified ribbon-wheel) contact.
In PFC (Figure 1), the melt is injected through a slit nozzle at the end of a pressurized crucible, and a melt puddle is stabilized by the small gap (typically less than 0.5 mm) between the nozzle and the spinning wheel. The melt puddle consists of an upstream meniscus maintained by the surface tension and a downstream meniscus formed by the momentum balance of the free surface. It is the stability of the melt puddle that determines the surface quality of the cast ribbons. The relevant process parameters include applied pressure (p), nozzle-slot breadth (S), nozzle/wheel gap (G), melt superheat, and wheel speed (U). Other relevant parameters include density ( ), surface tension (
), surface tension (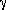 ), and viscosity of the liquid metal (µ).
), and viscosity of the liquid metal (µ).
The contact side of the solidified ribbon is often smooth, except at very high wheel speed; on the other hand, the free surface side often shows various roughness, such as dimpled, striated, herringbone, and wavy patterns under different processing conditions.3,4 One way to avoid these undesirable patterns is to cast the materials in a narrow processing window formed by a careful selection of inertia, surface tension, and viscous forces.3,4 However, in order to increase the robustness of PFC so that a wide range of thickness and width of ribbons and strips can be produced, it is necessary to control the surface quality and improve the contact heat transfer.
| Table II. Pressure and Force Estimations | ||
|---|---|---|
| Parameter | U=10 m/s (ribbon) | U=1 m/s (strip) |
| Overpressure (P) |
2,000 Pa | N/A |
| Static Pressure (  gz) (z = 5cm) gz) (z = 5cm) |
N/A | 1,128 Pa |
| Surface Tension (2 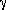 /G) /G) |
1,700 Pa | 1,700 Pa |
| Inertia Team (1/2  U2) U2) |
115,000 Pa | 1,150 Pa |
| Shear Stress (vU/T) |
100 Pa | 10 Pa |
| Centrifugal Force (  U2/Rw) U2/Rw) |
235,000 N/m3 | 2,350 N/m3 |
| Table III. Electromagnetic Properties of Coil and Aluminum Ribbon | |
|---|---|
| Conductivity |  = 3.77 x 107 (A/m-V) = 3.77 x 107 (A/m-V) |
| Permeability | µ = 1.26 x 10-6 (V-s/A-m) |
| Coil Diameter | D = 0.12m, 0.06m |
| Coil Turns | n = 1 |
| Coil Current | I = 500 A, 5,000 A (DC) |
| Wheel Speed | u = 0, 0.5, 1, 5, 10, 20, and 40 m/s |
Because the free surface and meniscus are mainly controlled by the momentum balance of pressure and surface tension, it is necessary to match the EM pressure with the static pressure and surface tension by choosing a magnetic flux of 0.05-0.1 T so that the EM pressure B2/2µ = 992-3,970 Pa. The EM Lorenz force will approximately match the centrifugal force in strip casting when U  1 m/s. Based on this simple order-of-magnitude analysis and these calculations, the chosen coil and EM parameters for aluminum are shown in Table III.
1 m/s. Based on this simple order-of-magnitude analysis and these calculations, the chosen coil and EM parameters for aluminum are shown in Table III.
A common way of treating the problem is to use the current vector potential ( ) in the finite-element (FE) formulation of quasisteady Maxwell's equations13 for the moving conductor (i.e., aluminum ribbon)
) in the finite-element (FE) formulation of quasisteady Maxwell's equations13 for the moving conductor (i.e., aluminum ribbon)
J =  x x  |
(1) |
The eddy-current density J (A/m2) induced in a conducting ribbon with a conductivity  by the electrical field E (volt) is represented as
by the electrical field E (volt) is represented as
J =  E E |
(2) |
The electric-filed E caused by the change of the magnetic field density B (Tesla) with time is given by Maxwell's equation as
 x E = x E = |  |
(3) |
By combining Equations 1-3 and considering the effect of the induced current, we obtain the governing equation for the moving ribbon with permeability µ as
 |
(4) |
 z. For simplicity in notation, we will use B (Tesla) and
z. For simplicity in notation, we will use B (Tesla) and  (A/m) to represent the z component of the magnetic field and current vector potential, respectively. Thus, Equation 4 becomes
(A/m) to represent the z component of the magnetic field and current vector potential, respectively. Thus, Equation 4 becomes
 |
(5) |
which indicates that there are two terms to contribute to  B/
B/ t—the movement of the ribbon (convective term) and the varying current (transient term) in electric coil
t—the movement of the ribbon (convective term) and the varying current (transient term) in electric coil
 |
(6) |
where U is the moving speed of the ribbon in x-direction. The second term on the right-hand side of Equation 6 is due to the change of the source current; subscript i is used to indicate the difference between this term and the first term. The first term is zero for static field (U = 0), while the second term is zero for a direct current EM coil.
The magnetic field B(t) generated by the EM coil has Br and Bz components that are given by Reference 14 as
 |
(7) |
 |
(8) |
where I is the current flowing through the coil
 |
(9) |
and K(k) and E(k) are, respectively, the complete elliptic integrals of the first and the second kinds, i.e.,
 |
(10) |
The parameters n and R are the number of turns and radius of the coil, respectively.
In the calculations, the eddy currents are assumed not to leak outside the finite length of the ribbon, which is large enough relative to the coil (i.e.,  = 0 along the entire edges of the ribbon). Once the eddy-current density is calculated, the Lorentz force density (N/m3) can be obtained from
= 0 along the entire edges of the ribbon). Once the eddy-current density is calculated, the Lorentz force density (N/m3) can be obtained from
| F = J x B | (11) |
where F is the Lorentz force density (N/m3). Since the eddy current J (x,y) is two-dimensional and B (r,z) is two-dimensional (2-D) in the (r,z) coordinate but three-dimensional (3-D) in the (x,y,z) coordinate, the Lorentz force becomes 3-D [i.e., F = F (x,y,z)].
 |
(12) |
where
 |
(13) |
 |
(14) |
 |
(15) |
and [N] is shape function, and h is the thickness of the ribbon. Both the modified implicit Euler method and Galerkin method are used to solve Equation 12. Let t denote a typical time in response so that tn+1 = tn +  t. Using the Euler method, Equation 12 can be rewritten as
t. Using the Euler method, Equation 12 can be rewritten as
| S(t)V(t) = F(t) | (16) |
where
S(t) = 2C/ t + D(t) t + D(t) |
(17) |
 |
(18) |
 |
(19) |
Using the Galerkin method, Equation 12 becomes
 |
(20) |
and
 |
(21) |
No significant difference is found between the calculated results from these two methods, but the Galerkin method takes less calculation time than the implicit Euler method.
To get Lorentz force, the following steps are taken chronologically:
 B/
B/ x,
x,  B/
B/ t.
t.
 from Equation 12 with the prescribed boundary conditions (i.e., no current leakage through the edges).
from Equation 12 with the prescribed boundary conditions (i.e., no current leakage through the edges).
The output file contains the final results, which include the current vector potential, the eddy current in x-y plane, and the Lorentz force in z- and x-y plane.
Figure 2 shows the eddy-current flux vectors induced in the ribbon as it travels at a speed of U = 10 m/s, a coil current of nI = 500A, and with a coil diameter of D = 0.12 m. The x = 0 location corresponds to the right (leading) edge of the 0.5 m (x direction) by 0.2 m (y direction) computational domain. The results show that the eddy current is induced shortly after the rectangular sheet enters under the coil at t = 0.004 s (Figure 2a). Figure 2b shows a strong eddy current directly under the coil; strong eddy currents are also seen near the leading edge of the ribbon due to the initial transient and edge effect. A steady-state condition is reached after t = 0.016 s (Figure 2c), when the leading edge of the rectangular sheet travels past the coil center by 0.16 m (coil diameter = 0.12 m). The induced eddy current is in the opposite direction of the applied coil current with a maximum value of 2.48 x 105 A/m2. However, the eddy current near the coil center is almost zero, forming a dead zone.
The Lorentz force density is 3-D due to the cross product of the 2-D eddy current and the 3-D magnetic flux. Figure 3 show the force density vectors in the x-y plane at t = 0.016 s when the quasisteady condition is reached. The force in the x-y plane appears to point toward the center of the coil. The net Fy force is equal to zero due to symmetry. The net Fx force is negative, because stronger eddy currents are found to be ahead of the coil rather than in the region behind the coil (i.e., the drag force in the opposite direction of the ribbon motion is induced).
Figure 4 shows the vertical force Fz (x,y,t) in a 3-D and 2-D contour plot at t = 0.03 s, after the quasisteady condition is reached. The force distribution appears to be symmetrical with a maximum lift (downward and repulsive) force just under the coil perimeter. The maximum Fz is 2,480 N/m3 (Figure 4a) for U = 10 m/s, nI = 500 A, D = 0.12 m. When the current times the number of coils (nI) is increased to 5,000 A, both the magnetic flux and the eddy current are increased tenfold. Consequently, the force is increased by one hundred times to 248,000 N/m3 (Figure 4b), which matches the centrifugal force of ribbon casting at U = 10 m/s in Table II.
Since the lift force is almost zero near the center of the coil, termed the "dead zone" (Figure 4a and Figure 4b), it was decided to reduce the coil diameter by one half to 0.06 m, while keeping other parameters constant. As a result, the force distribution in Figure 4c is more uniform without the dead zone near the center. This suggests that multiple coils with different diameters, such as cone-shaped spiral coils, may be used to provide a uniform force on the moving ribbon.
The lift (FL = -Fz) and drag (FD = -Fx) forces versus time are shown in Figure 5. Since the current-vector potential field (H) is assumed to be zero at t = 0, the initial forces are also zero. As time progresses, the ribbon moves under the coil, the eddy current is induced, and Lorentz force is developed. The lift force fluctuates with time initially and settles to a quasisteady-state value at t = 0.016 s, when the leading edge of the computational domain travels 0.16 m past the coil center. The fluctuations are caused by a combination of the initial condition ( = 0) and the edge effect (
= 0) and the edge effect ( = constant, no leakage). When the coil diameter is reduced to one half, it only takes 0.08 s (a distance of 0.08 m) to reach a quasisteady state. This is attributed to the reduced edge effect by the smaller coil (D = 0.06 m) within the 0.5 m x 0.2 m computational domain. It is noteworthy to mention that the quasisteady condition is reached sooner at high U, because the settling time is determined by the traveling distance rather than the traveling time. The transient behavior is similar to the start-up period during the actual production of ribbons and strips. A certain length of ribbons with irregular shapes in the leading edge is produced before a quasisteady operation is reached.
= constant, no leakage). When the coil diameter is reduced to one half, it only takes 0.08 s (a distance of 0.08 m) to reach a quasisteady state. This is attributed to the reduced edge effect by the smaller coil (D = 0.06 m) within the 0.5 m x 0.2 m computational domain. It is noteworthy to mention that the quasisteady condition is reached sooner at high U, because the settling time is determined by the traveling distance rather than the traveling time. The transient behavior is similar to the start-up period during the actual production of ribbons and strips. A certain length of ribbons with irregular shapes in the leading edge is produced before a quasisteady operation is reached.
Figure 6 shows the quasisteady lift (FL = -Fz) and drag (FD = -Fx) versus the ribbon speed (U). The lift and drag forces are zero at U = 0, since direct current is applied. The drag force (lower curve) increases to a local maximum at U = 0.5 m/s, then decreases slowly as U increases. The lift force (upper curve) increases almost linearly with U at low speed, increases more slowly at moderate speed, and finally levels off at high speed (U > 25 m/s). The results are similar to those obtained in References 15 and 16, in which the magnets move relative to the still conductors. The effect of U B/
B/ x in the present model is modeled by the U x B term in the electrical field of the still conductor.15,16 In the case of U = 0 m/s, it is necessary to use the alternating current to generate the eddy current and, thus, the Lorentz force.
x in the present model is modeled by the U x B term in the electrical field of the still conductor.15,16 In the case of U = 0 m/s, it is necessary to use the alternating current to generate the eddy current and, thus, the Lorentz force.
The EM probes and thin-foil force sensors are being developed to validate these modeling results. The EM force will be combined with the fluid-flow and solidification models to predict the transport phenomena in melt spinning and strip casting. The present model may be extended to twin-roll casting for meniscus shape control and edgeless dam design.17-19
K. Zhang earned his Ph.D. in materials science from Northwest Polytechnic University, China, in 1990. He is now a Ph.D. candidate in mechanical engineering at Temple University.
M.N.O. Sadiku earned his Ph.D. from Tennessee Tech University in 1984. He is currently a full professor in the Department of Electrical Engineering and Computers at Temple University.
A.A. Tseng earned his Ph.D. from Georgia Institute of Technology in 1978. He is currently a professor in the Mechanical and Aerospace Engineering Department and Laboratory Engineering Director of Manufacturing Institute, Arizona State University. Dr. Tseng is also a member of TMS.
Direct questions about this or any other JOM page to jom@tms.org.
| Search | TMS Document Center | Subscriptions | Other Hypertext Articles | JOM | TMS OnLine |
|---|