 |
49 (8) (1997), pp. 35-39. JOM is a publication of The Minerals, Metals & Materials Society |
|---|
 |
49 (8) (1997), pp. 35-39. JOM is a publication of The Minerals, Metals & Materials Society |
|---|
| CONTENTS |
|---|
|
|
INTRODUCTION
In-situ composites are multiphase materials where the reinforcing phase is synthesized within the matrix during composite fabrication. This contrasts with ex-situ composites where the reinforcing phase is synthesized separately and then inserted into the matrix during a secondary process such as infiltration or powder processing. In-situ processes can create a variety of reinforcement morphologies, ranging from discontinuous to continuous, and the reinforcement may be either ductile or ceramic phases.
There are a number of processes and classes of in-situ composites, including processes where the precipitation of reinforcements occurs in the liquid state and processes where precipitation occurs in the solid state.1 Processes in which precipitation occurs in the liquid state include those occurring with low undercoolings, such as traditional and directionally solidified eutectics; rapid solidification in which a supersaturation is created by rapidly cooling a liquid with the reinforcement constituents already in solution; and processes in which a large supersaturation is created by rapidly bringing the constituents of the reinforcement together to react. These latter processes include the XDTM,2,4 Mixalloy,5 reactive-gas injection (Drexal process),6,7 reactive sintering,8 reactive hot isostatic pressing (HIPing), and plasma conversion9 processes. Solid-state in-situ processes include internal oxidization,10 displacement reactions,11 reactive milling, mechanical alloying, and cryomilling.12 There are also traditional eutectoid reactions that can be considered solid-state in-situ reactions if an alloy of ferrite and cementite is considered a composite.
Generally, the reinforcements in discontinuously reinforced metallic- or intermetallic-matrix in-situ composites are on the order of 0.5-5 µm, and volume fractions range from 0-50 vol.%. The potential advantages of in-situ composites as compared to discontinuous metal-ceramic composites produced by ex-situ methods include:
| STRENGTHENING MECHANISMS | ||||||||||
| Several possible explanations for increases in yield strength of discontinuously reinforced composites with equiaxed particles in the range 0.5-5 µm in diameter have been proposed in recent reviews.13,14
Continuum-mechanics models of composite behavior assume that load is transferred from the matrix to a nonplastically deforming reinforcement. One such model, shear-lag theory, assumes that load transfer occurs between a high-aspect-ratio reinforcement and the matrix by means of shear stresses at the particle-matrix interface.15 According to a modified shear-lag theory, which also accounts for load transfer at the particle ends,16,17 the yield stress of the composite
where  ym is the yield stress of the unreinforced matrix, L is the length of the particle perpendicular to the applied stress, t is the length of the particle parallel to the applied stress, A is the particle-aspect ratio, and f is the particle-volume fraction. For the equiaxed particles present in most in-situ composites, Equation A reduces to ym is the yield stress of the unreinforced matrix, L is the length of the particle perpendicular to the applied stress, t is the length of the particle parallel to the applied stress, A is the particle-aspect ratio, and f is the particle-volume fraction. For the equiaxed particles present in most in-situ composites, Equation A reduces to
It is important to note that this form of the equation is linear, with a very modest increase in  y with increasing volume fraction, and there is no dependence of yield stress on particle size or microstructural scale. Finite-element solutions to the elastic-plastic continuum model for the problem of regularly spaced spheres have been obtained for two dimensions18 and three dimensions.19 These models yield similar results to the shear-lag theory at low volume fractions, but the elastic-plastic models predict a greater increase in strength above about 20 vol.%. y with increasing volume fraction, and there is no dependence of yield stress on particle size or microstructural scale. Finite-element solutions to the elastic-plastic continuum model for the problem of regularly spaced spheres have been obtained for two dimensions18 and three dimensions.19 These models yield similar results to the shear-lag theory at low volume fractions, but the elastic-plastic models predict a greater increase in strength above about 20 vol.%.
A great deal of work has been performed on aluminum alloys reinforced ex-situ by SiC particles, plates, and whiskers. In many of these composites, dislocations are generated in the alloy matrix upon cooling or quenching from the processing or solutionizing temperature, due to a mismatch of the coefficient of thermal expansion (CTE) between the matrix and SiC reinforcement.20,21 The higher dislocation density increases the strength of the alloy.22,23 The amount of dislocation generation is affected by CTE, particle size, particle-volume fraction, and matrix strength.24 Single Dislocation-Particle Interaction Model: Orowan Strengthening Gliding dislocation can bow between small impenetrable particles and bypass them, leaving behind an Orowan loop. The effect of this process on the yield stress of the material is described by the Orowan relationship. For polycrystalline materials, this is
where M is the Taylor factor, µ is the shear modulus, b is the Burgers vector, v is the Poisson's ratio, r is the effective radius of the particles, ro is the cut-off radius, and  is the mean interparticle separation on the slip plane.25 is the mean interparticle separation on the slip plane.25
Multiple Dislocation-Particle Interaction Models Dislocation Pile-Up Models The yield stress of single-phase polycrystalline materials is phenomenologically observed to be proportional to d-1/2, where d is the grain diameter. This leads to the relation
known as the Hall-Petch relationship, which arose from experimental observations. Typically  o is rationalized as either a frictional stress resisting the motion of gliding dislocations or as an internal back stress. ky is the Hall-Petch slope, which is considered to be a measure of the resistance of the grain boundary to slip transfer. Typical values of ky at room temperature are on the order of 0.05-0.1 MPa o is rationalized as either a frictional stress resisting the motion of gliding dislocations or as an internal back stress. ky is the Hall-Petch slope, which is considered to be a measure of the resistance of the grain boundary to slip transfer. Typical values of ky at room temperature are on the order of 0.05-0.1 MPa  for face-centered cubic (f.c.c.) metals and 0.3-1.8 MPa for face-centered cubic (f.c.c.) metals and 0.3-1.8 MPa  for body-centered cubic (b.c.c.) metals. Although most studies have been carried out at ambient temperature, results indicate that the Hall-Petch relationship can also be used at elevated temperatures26 where ky decreases with increasing temperature. for body-centered cubic (b.c.c.) metals. Although most studies have been carried out at ambient temperature, results indicate that the Hall-Petch relationship can also be used at elevated temperatures26 where ky decreases with increasing temperature.
The same d-1/2 dependence of the yield stress has been observed in two-phase alloys where d is the characteristic microstructural dimension (i.e., the dimension that governs slip distance). Examples include drawn ferrite, where d is the dislocation cell size; drawn pearlite, where d is the interlamellar spacing of carbide; and polygonized aluminum, where d is the cell size. A very informative example is that of the competitive effects of cementite particles, grain boundaries, and subgrain boundaries on the behavior of spheroidized cementite in a ferrite matrix as analyzed by Anand and Gurland.27 Another example is the strengthening of deformation-processed composites such as drawn or rolled Cu-Nb, where the strength increase has been attributed to direct blocking of the dislocation motion by the interphase boundaries leading to a If the grain boundaries or subgrain boundaries are obstacles to dislocation motion, then the grain or subgrain size is the characteristic microstructural dimension. However, if particles are obstacles to dislocation motion, then the interparticle separation is the characteristic microstructural dimension. In either case, when dislocation pile-up is the operative strengthening mechanism, an inverse square root dependence on the characteristic microstructural dimension will be observed. When grain size and interparticle spacing have similar dimensions, dislocation pile-ups at both particle-matrix interfaces and grain boundaries may contribute. In these situations, the ease of dislocation annihilation or generation at a particular interface is at issue. Thus, the behavior of the interphase barrier may be as important as the spacing of these interfaces. Forest Hardening Models
Another effect that dislocations may have is their role on work-hardening behavior at small strains. Kamat et al.31 have examined the tensile properties of 2024 and 2014 aluminum alloys reinforced with equiaxed alumina particles and suggest that dislocation tangles form around particles at small strains because of plastic incompatibility. These geometrically necessary dislocations link up to form dislocation cells with a diameter proportional to the interparticle spacing
where  is a proportionality constant. Thus, it is possible in some composites that the reinforcement of the matrix does not significantly alter the onset of plastic deformation. Instead, the observed increase in the 0.2% offset yield stress is due to an increase in the work-hardening rate at small strains.13 In these alloys, a is a proportionality constant. Thus, it is possible in some composites that the reinforcement of the matrix does not significantly alter the onset of plastic deformation. Instead, the observed increase in the 0.2% offset yield stress is due to an increase in the work-hardening rate at small strains.13 In these alloys, a  -1 dependence of the 0.2% offset yield stress should be observed. -1 dependence of the 0.2% offset yield stress should be observed.
|
These benefits may not be realized for all systems, but tend to be very system and property specific.
In-situ composites also have disadvantages. The synthesis of an in-situ reinforcement is typically by a precipitation process, and, as such, the choice of in-situ reinforcements is limited to particles that are thermodynamically stable within a particular matrix. The size and shape of particles are controlled by nucleation and growth processes, so although significant flexibility may be available during processing and synthesis, the size and shape are ultimately determined by the kinetics of the system instead of the ex-situ synthesis and processing of the reinforcements. Although particle distribution may be more uniform, the potential also exists for the pushing of fine particles during solidification.
 0.5 of the matrix solidus temperature). The yield stress versus temperature curves are displaced to higher stresses with increasing particle-volume fraction, although at relatively high temperatures (300°C), the yield stress of all the materials falls to a similar value. The elongation to fracture is constant with increasing temperature, with a rapid increase in elongation at higher temperatures. The increase in elongation at high temperatures is more pronounced as the volume fraction of TiB2 increases. Thus, elongation decreases with increasing particle loading at low temperatures, and increases with increasing particle loading at high temperatures.
0.5 of the matrix solidus temperature). The yield stress versus temperature curves are displaced to higher stresses with increasing particle-volume fraction, although at relatively high temperatures (300°C), the yield stress of all the materials falls to a similar value. The elongation to fracture is constant with increasing temperature, with a rapid increase in elongation at higher temperatures. The increase in elongation at high temperatures is more pronounced as the volume fraction of TiB2 increases. Thus, elongation decreases with increasing particle loading at low temperatures, and increases with increasing particle loading at high temperatures.
The proportional limit and 0.2% offset yield stress of Al-4Cu-1.5Mg composites containing 0, 2, 5, 10, and 15 vol.% TiB2 at two average particle diameters are shown in Figure 2 for tensile tests conducted at room temperature. These alloys were extruded, solutionized at 493°C, water quenched, and then allowed to naturally age at room temperature. This heat treatment produces a dispersion of very fine Guinier-Preston (GP) zones that are sheared by the movement of dislocations such that the matrix deforms by planar slip. The yield stress increases with increasing particle-volume fraction. At any given particle-volume fraction, the composites with the small particles exhibit higher strength than the composites with larger particles. Note that the yield stress and the proportional limit increase at a similar rate with increasing volume fraction of TiB2. Thus, the observed increase in strength is due to an increase in the initial resistance to the movement of dislocations and not a difference in the initial strain-hardening rate.
The applicability of the various characteristic slip-length models can be examined by plotting the yield stress against the various microstructural dimensions. The grain size for these alloys had been experimentally measured and is larger than the interparticle spacing by a factor of 3-5, depending on the alloy. In Figure 3, the yield stress is plotted against the inverse square root of the measured interparticle spacing,  -1/2, with a least-square fit of the data.
-1/2, with a least-square fit of the data.
The slope obtained from a similar fit against  -1 yields a slope that differs from the Orowan slope predicted by Equation C in the sidebar by several orders of magnitude; thus, the observed dependence on particle spacing is not due to Orowan strengthening. Since particles of different size produce different amounts of strengthening, continuum models can be eliminated since they can not account for the observed particle-size effect. Further, transmission electron microscopy examination showed similar dislocation densities for reinforced and unreinforced alloys; therefore, differences in dislocation density are not responsible for the observed strengthening. Shear-lag theory for these equiaxed particles (Equation B) predicts an increase in the yield stress that is significantly smaller than what is observed. Hence, the data suggest that the strength increase in these composites is due to dislocation pile-ups through an interphase barrier-strengthening mechanism.
-1 yields a slope that differs from the Orowan slope predicted by Equation C in the sidebar by several orders of magnitude; thus, the observed dependence on particle spacing is not due to Orowan strengthening. Since particles of different size produce different amounts of strengthening, continuum models can be eliminated since they can not account for the observed particle-size effect. Further, transmission electron microscopy examination showed similar dislocation densities for reinforced and unreinforced alloys; therefore, differences in dislocation density are not responsible for the observed strengthening. Shear-lag theory for these equiaxed particles (Equation B) predicts an increase in the yield stress that is significantly smaller than what is observed. Hence, the data suggest that the strength increase in these composites is due to dislocation pile-ups through an interphase barrier-strengthening mechanism.
Sahoo and Koczak examined a series of Al-4.5Cu alloys reinforced with 0-11 vol.% TiC produced by reactive gas injection.32 They found increases in tensile yield and ultimate tensile strength on the order of 200 MPa, significantly greater than what would be predicted by the observed reduction in grain size. These results are consistent with the interphase-barrier strengthening.
Although the operative strengthening mechanisms have not been identified, other discontinuously reinforced aluminum-matrix in-situ composites for which strength and tensile data have been published include Al-5Mg and Al-5Cu reinforced with 5 vol.% or 10 vol.% TiC,33 aluminum reinforced with 20 vol.% TiB2, 34 aluminum simultaneously reinforced with Al2O3 and TiB2,35 Al-5.8Cu-0.2Mg-0.2Mn (2519) reinforced with 4.4 vol.% or 6.4 vol.% TiC,36 and Al-6.4Cu-1.4Li-0.3Ag-0.4Mg-0.15Zr (2195) reinforced with 4 vol.% TiB2.37 The compressive and flexural properties of aluminum reinforced with 30 vol.% TiB2, TiC, or a mixture of TiB2 and TiC have also been examined.38
In Figure 5, the compressive yield stresses of the 13 composites containing 15, 30, or 45 vol.% of the indicated particles are plotted versus the inverse square root of the measured planar interparticle spacing for test temperatures of 1,000°C and 1,200°C. For the unreinforced alloy, the grain size is taken as the effective slip distance and is used instead of  in these plots. Values of ky ranged from 2.8 MPa
in these plots. Values of ky ranged from 2.8 MPa at 800° to 1.4 MPa
at 800° to 1.4 MPa at 1,200°C. These values are somewhat higher than the ky values of 0.05-1.3 MPa
at 1,200°C. These values are somewhat higher than the ky values of 0.05-1.3 MPa determined for conventional metals at room temperature, but are consistent with particles acting as strong obstacles and with the difficulty of renucleating slip on the other side of a nondeforming particle. Such a high ky value would also be expected in materials with a limited slip number of systems such as MoSi2. Values of so decreased from 280 MPa at 800°C to 50 MPa at 1,400°C. Although a dislocation-strengthening model is applied to MoSi2 below its ductile-to-brittle transition temperature of approximately 1,300°C,41 a dislocation-based strengthening argument is not inconsistent, as there is ample evidence of dislocation activity below 1,300°C.42,43
determined for conventional metals at room temperature, but are consistent with particles acting as strong obstacles and with the difficulty of renucleating slip on the other side of a nondeforming particle. Such a high ky value would also be expected in materials with a limited slip number of systems such as MoSi2. Values of so decreased from 280 MPa at 800°C to 50 MPa at 1,400°C. Although a dislocation-strengthening model is applied to MoSi2 below its ductile-to-brittle transition temperature of approximately 1,300°C,41 a dislocation-based strengthening argument is not inconsistent, as there is ample evidence of dislocation activity below 1,300°C.42,43
The fact that the ZrB2 and HfB2 particles are plate shaped while the TiB2 and SiC are nearly equiaxed particles is accounted for through the use of the experimentally measured  . It should be noted that as the aspect ratio of the reinforcements becomes very large, load transfer would be expected to become a significant strengthening mechanism. The contribution of strengthening due to load transfer would overwhelm the role of dislocation slip in the matrix only when the aspect ratio becomes extremely large.
. It should be noted that as the aspect ratio of the reinforcements becomes very large, load transfer would be expected to become a significant strengthening mechanism. The contribution of strengthening due to load transfer would overwhelm the role of dislocation slip in the matrix only when the aspect ratio becomes extremely large.
Flexural stress-strain curves for MoSi2 reinforced with 30 vol.% SiC, 30 vol.% TiB2, or 30 vol.% HfB2 and an unreinforced MoSi2 sample are shown in Figure 6.44 The origins of neighboring curves have been displaced for clarity. Although not shown, the behavior of the alloys at 1,000°C is nearly identical to the behavior exhibited at 1,200°C. At 1,200°C, the stress-strain behavior is linearly elastic with fracture prior to yield. At 1,300°C, the TiB2 and HfB2 alloys undergo approximately 0.2% outer-fiber plastic strains prior to fracture, while the SiC-reinforced alloy exhibits about 1.0% outer-fiber plastic strains. The unreinforced alloy fractures prior to any plasticity at 1,300°C. At 1,400°C, all four alloys exhibit significant ductility and do not fracture prior to termination of the test. The apparent ductile-to-brittle transition temperature for the reinforced and unreinforced samples was approximately 1,300°C. To a first approximation, this transition temperature appears to be independent of particle type but is dependent on the MoSi2 matrix grain size. These tests not only illustrate the effect of reinforcements on strength, but also their effect on the work-hardening rate of the composite.
The flexural strength of in-situ MoSi2 composites reinforced with SiC produced by a solid-state displacement reaction have also been examined.11,45 For composites with between 30-67 vol.% SiC, larger SiC particles resulted in higher strength at elevated temperature, while a higher SiC volume fraction resulted in reduced strength. These trends were attributed to the SiC phase becoming continuous in these composites at large volume-particle sizes and high volume fractions.
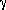 Ti-Al alloys containing 0, 7, or 12 vol.% of TiB2 particulates produced by the XDTM process.46,47 They found that the strength of the composites was a sum of three different components: the strength of the unreinforced alloy, a direct strength increment due to the presence of the reinforcement, and an indirect strength increment (or decrement) due to the effect the reinforcement on the microstructure of the matrix (including grain size, solid-solution strengthening, and changes in the relative proportions of
Ti-Al alloys containing 0, 7, or 12 vol.% of TiB2 particulates produced by the XDTM process.46,47 They found that the strength of the composites was a sum of three different components: the strength of the unreinforced alloy, a direct strength increment due to the presence of the reinforcement, and an indirect strength increment (or decrement) due to the effect the reinforcement on the microstructure of the matrix (including grain size, solid-solution strengthening, and changes in the relative proportions of  2 and
2 and 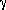 in the matrix). The direct strengthening due to the reinforcements was found to be proportional to the inverse square root of the interparticle spacing, implying an interphase-barrier strengthening mechanism.
in the matrix). The direct strengthening due to the reinforcements was found to be proportional to the inverse square root of the interparticle spacing, implying an interphase-barrier strengthening mechanism.
Near-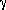 Ti-Al alloys were also in-situ-reinforced with 40 vol.% and 50 vol.% TiB2.48 The strength of these alloys, with corrections to account for alloy chemistry, were found to lie on the same strength versus inverse square root of the interparticle spacing curve as the 7% and 12% alloys.
Ti-Al alloys were also in-situ-reinforced with 40 vol.% and 50 vol.% TiB2.48 The strength of these alloys, with corrections to account for alloy chemistry, were found to lie on the same strength versus inverse square root of the interparticle spacing curve as the 7% and 12% alloys.
Other discontinuously reinforced intermetallic-matrix in-situ composites for which strength data have been published include Ni-Al reinforced with 20 vol.% TiC49 and Nb-26Ti-48Al (at.%) reinforced with borides and carbides.50
In-situ copper-matrix composites reinforced with group IV borides and carbides have been produced by the XDTM process. The tensile yield stress of copper reinforced in-situ with between 7.5 vol.% and 20 vol.% ZrB2 is shown in Figure 7. These results are very similar to those shown for the Al-4Cu-1.5Mg/TiB2 composites shown in Figure 1; in creases in reinforcement volume fraction provide increased strength. The elongation to fracture at room temperature of these composites range from 12% for the 7.5 vol.% composite down to 2% for the 20 vol.% composite, demonstrating the excellent thermal stability of this material. Fracture occurs by void nucleation at the particle/matrix interface, which is then followed by void growth and coalescence.
Samples of Cu-15ZrB2 (vol.%) were heat treated in vacuum at temperatures 68-93% of the melting point for times up to 100 hours. These temperatures are in far excess of any likely use temperature. The room-temperature yield stress of this material as a function of time at temperature is shown in Figure 8. At the highest aging temperatures, there is a drop in the yield strength during the initial few hours, but after that the strength (and, by inference, the microstructure) remain relatively unchanged. The elongation to failure of these same materials showed relatively little change for the 650°C heat treatment and a modest increase from 2% up to 3% for the material heat treated at 980°C.
 |
| Figure 6. The stress-strain curves for XDTM MoSi2 composites at elevated temperature in a four-point bend test. Samples were tested in air at a strain rate of 2 X 10-5 s-1. |
 to 25 MPa
to 25 MPa . The particle size apparently had no effect on toughness, but the smaller particle material had a very nonuniform distribution of particles (due to particle pushing during solidification), which may have masked any effect. For the 1.3 µm materials, the results obtained followed the prediction of Rice and Johnson52 in the manner of Han and Rosenfield53
. The particle size apparently had no effect on toughness, but the smaller particle material had a very nonuniform distribution of particles (due to particle pushing during solidification), which may have masked any effect. For the 1.3 µm materials, the results obtained followed the prediction of Rice and Johnson52 in the manner of Han and Rosenfield53
KIC = k 
 (1)
(1)
where E is the Young's modulus,  y is the yield stress,
y is the yield stress,  the interparticle spacing, and k depends on the nature of void initiation. Assuming a ductile void growth model, k is equal to the particle diameter divided by the interparticle spacing.
the interparticle spacing, and k depends on the nature of void initiation. Assuming a ductile void growth model, k is equal to the particle diameter divided by the interparticle spacing.
Kumar, Mannan, and Viswanadham examined the influence of TiB2 on the toughness of NiAl.54 They found that the addition of TiB2 particles to stoichiometric NiAl did not significantly affect fracture toughness, while the addition of TiB2 to nickel-rich NiAl degraded toughness. Another in-situ composite examined is MoSi2 with SiC.11
 ' precipitates). Although the morphology of the precipitates in the aluminum matrix was observed to significantly influence the cyclic response of the composites, it generally had no influence on the fatigue life under either plastic-strain-controlled or stress-controlled fatigue testing. The influence of matrix microstructure on the cyclic response of the composite was similar to the behavior of unreinforced alloys.
' precipitates). Although the morphology of the precipitates in the aluminum matrix was observed to significantly influence the cyclic response of the composites, it generally had no influence on the fatigue life under either plastic-strain-controlled or stress-controlled fatigue testing. The influence of matrix microstructure on the cyclic response of the composite was similar to the behavior of unreinforced alloys.
There have been a number of studies that have examined the creep behavior of in-situ-reinforced intermetallic-matrix composites. These include near-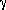 Ti-Al reinforced with TiB258-60 or a mix of TiB2 and Ti2AlN,59 NiAl with TiB2,61 NiAl with AlN,62-64 and MoSi2 with SiC.65,66 In general, reducing the grain size of the matrix contributes to higher creep rates, while increasing the volume fraction of the reinforcement contributes to lower creep rates. For most of these intermetallic-matrix composites, the presence of the reinforcing particles results in small grain sizes (on the order of the interparticle spacing), and creep is degraded when compared to an unreinforced material. Creep was improved by the presence of the particles in the aluminum composites that Krajewski et. al examined, which had a relatively large grain size. Thus, the key to good creep behavior for these intermetallic-matrix composites would appear to not only be to provide reinforcing phases, but to also process in order to obtain large grain sizes (something with which the reinforcing particles will interfere).
Ti-Al reinforced with TiB258-60 or a mix of TiB2 and Ti2AlN,59 NiAl with TiB2,61 NiAl with AlN,62-64 and MoSi2 with SiC.65,66 In general, reducing the grain size of the matrix contributes to higher creep rates, while increasing the volume fraction of the reinforcement contributes to lower creep rates. For most of these intermetallic-matrix composites, the presence of the reinforcing particles results in small grain sizes (on the order of the interparticle spacing), and creep is degraded when compared to an unreinforced material. Creep was improved by the presence of the particles in the aluminum composites that Krajewski et. al examined, which had a relatively large grain size. Thus, the key to good creep behavior for these intermetallic-matrix composites would appear to not only be to provide reinforcing phases, but to also process in order to obtain large grain sizes (something with which the reinforcing particles will interfere).
1. S.G. Fishman, In-Situ Composites: Science and Technology, ed. M. Singh and D. Lewis (Warrendale, PA: TMS, 1994), p. 1.
2. J.M. Brupbacher, L. Christodoulou, and D.C. Nagle, U.S. patent 4,710,348 (1987).
3. L. Christodoulou, D.C. Nagle, and J.M. Brupbacher, U.S. patent 4,774,052 (1988).
4. D.C. Nagle, J.M. Brupbacher, and L. Christodoulou, U.S. patent 4,916,029 (1990).
5. N.P. Suh, U.S. patent 4,278,622 (1981).
6. M.J. Koczak and K.S. Kumar, U.S. patent 4,808,372 (1989).
7. V. Shtessel, S. Sampath, and M. Koczak, In-Situ Composites: Science and Technology, ed. M. Singh and D. Lewis (Warrendale, PA: TMS, 1994), p. 37.
8. S.D. Dunmead et al., U.S. patent 4,909,842 (1990).
9. P.R. Taylor and M. Manrique, Processing and Fabrication of Advanced Materials IV, ed. T.S. Srivatsan and J.J. Moore (Warrendale, PA: TMS, 1996), p. 827.
10. C.R. Cupp, Progress in Metal Physics, 4 (1953), p. 151.
11. C.H. Henager, Jr., J.L. Brimhall, and L.N. Brush, Mater. Sci. Eng., A195 (1995), p. 65.
12. M.J. Luton et al., Multicomponent Ultrafine Microstructures, Mater. Res. Soc. Symp. Proc., 132, ed. L.E. McCandis et al. (Pittsburg, PA: MRS, 1989), p. 79.
13. R.M. Aikin, Jr., and L. Christodoulou, Scripta Metall., 25 (1991), p. 9.
14. M. Taya, Mater. Trans. JIM, 32 (1991), p. 1.
15. A. Kelly, Strong Solids (Oxford, U.K.: Clarendon Press, 1966), p. 123.
16. V.C. Nardone and K.M. Prewo, Scripta Metall., 20 (1986), p. 43.
17. V.C. Nardone, Scripta Metall., 21 (1987), p. 1313.
18. G. Bao, J.W. Hutchinson, and R.M. McMeeking, Acta Metall. Mater., 39 (1991), p. 1871.
19. C.L. Hom and R.M. McMeeking, Int. J. Plasticity, 7 (1991), p. 255.
20. R.J. Arsenault and R.M. Fisher, Scripta Metall., 17(1983), p. 67.
21. Y. Flom and R.J. Arsenault, Mater. Sci. Eng., 75 (1985), p. 151.
22. R.J. Arsenault and N. Shi, Mater. Sci. Eng, 81 (1986), p. 175.
23. M. Volgelsang, R.J. Arsenault, and R.M. Fisher, Metall. Trans. A, 17 (1986), p. 379.
24. C.T. Kim, J.K. Lee, and M.R. Plichta, Metall. Trans. A, 21 (1990), p. 673.
25. P.M. Kelly, Int. Metall. Rev., 18 (1973), p. 31.
26. M.E. Kassner and X. Li, Scripta Metall., 25 (1991), p. 2833.
27. L. Anand and J. Gurland, Metall. Trans. A, 7 (1976), p. 191.
28. G. Wassermann, Proc. 2nd Int. Conf. on the Strength of Metals and Alloys (Metals Park, OH: ASM, 1970), p. 1188.
29. P.D. Funkenbusch and T.H. Courtney, Scripta Metall., 15 (1981), p. 1349.
30. W.A. Spitzig, A.R. Pelton, and F.C. Laabs, Acta Metall., 35 (1987), p. 2427.
31. S.V. Kamat, J.P. Hirth, and R. Mehrabian, Acta Metall., 37 (1989), p. 2395.
32. P. Sahoo and M.J. Koczak, Mater. Sci. Eng., A131 (1991), p. 69.
33. H. Nakata, T. Choh, and N. Kanetake, J. Mater. Sci., 30 (1995), p. 1719.
34. A.K. Kuruvilla et al., Sripta Metall., 24 (1990), p. 873.
35. Z.Y. Ma et al., Scripta Metall., 31 (1994), p. 635.
36. M.K. Premkumar and M.G. Chu, Mater. Sci. Eng., A202 (1995), p. 172.
37. T.J. Langan and J.R. Pickens, Scripta Metall., 25 (1991), p. 1587.
38. I. Gotman, M.J. Koczak, and E. Shtessel, Mater. Sci. Eng., A187 (1994), p. 189.
39. R.M. Aikin, Jr., Ceram. Eng. Sci. Proc., 12 (1991), p. 1643.
40. R.M. Aikin, Jr., Mater. Sci. Eng., A155 (1992), p. 121.
41. R.M. Aikin, Jr., Scripta Metall., 26 (1992), p. 1025.
42. S.A. Maloy et al., Acta Metall. Mater., 40 (1992), p. 3159.
43. S.A. Maloy, T.E. Mitchell, and A.H. Heuer, Acta Metall. Mater., 43 (1995), p. 657.
44. R.M. Aikin, Jr., International Symp. on Structural Intermetallics, ed. R. Darolia et al. (Warrendale, PA: TMS, 1993), p. 791.
45. C.H. Henager, Jr., J.L. Brimhall, and J.P. Hirth, Mater. Sci. Eng., A155 (1992), p. 109.
46. S.L. Kampe et al., Metall. Trans. A, 25 (1994), p. 2181.
47. S.L. Kampe et al., Intermetallic Matrix Composites III, Mat. Res. Soc. Symp. Poc., 350, ed. J.A. Graves, R.R. Bowman, and J.J. Lewandowski (Pittsburgh, PA: MRS, 1994), p. 159.
48. M.L. VanMeter, S.L. Kampe, and L. Christodoulou, Scripta Met., 34 (1996), p. 1251.
49. Z.P. Xing et al., Metall. Trans. A, 28 (1997), p. 1079.
50. R.M. Aikin, Jr., P.E. McCubbin, and L. Christodoulou, Intermetallic Matrix Composites, MRS Symp. Proc., 194, ed. D.L. Anton et al. (Pittsburgh, PA: MRS, 1990), p. 307.
51. N.C. Beck Tan, R.M. Aikin, Jr., and R.M. Briber, Metall. Trans. A, 25 (1994), p. 2461.
52. J.R. Rice and M.A. Johnson, Inelastic Behavior of Solids, ed. M.F. Kannine et al. (New York: McGraw-Hill, 1980), p. 641.
53. G.T. Hahn and A.R. Rosenfield, Metall. Trans. A, 6 (1975), p. 653.
54. K.S. Kumar, S.K. Mannan, and R.K. Viswanadham, Acta Metall., 40 (1992), p. 1201.
55. G.M. Vyletel, D.C. Van Aken, and J.E. Allison, Scripta Metall., 25 (1991), p. 2405.
56. P.E. Krajewski, J.W. Jones, and J.E. Allison, Metall. Trans. A, 26 (1995), p. 3107.
57. P.E. Krajewski, J.E. Allison, and J.W. Jones, Metall. Trans. A, 24 (1993), p. 2731.
58. S.L. Kampe, J.K. Bryant, and L. Christodoulou, Metall. Trans. A, 22 (1991), p. 447.
59. P.L. Martin et al., Proc. Fourth Int. Conf. On Creep and Fracture of Engineering Materials and Structures (London: IOM, 1990), p. 265.
60. K. Sadananda et al., International Symp. on Structural Intermetallics, ed. R. Darolia et al. (Warrendale, PA: TMS, 1993), p. 809.
61. J.D. Whittenberger et al., J. Mater. Sci., 25 (1990), p. 35.
62. J.D. Whittenberger, E. Arzt, and M.J. Luton, J. Mater. Res., 5 (1990), p. 2819.
63. J.D. Whittenberger, E. Arzt, and M.J. Luton, Scripta Metall., 26 (1992), p. 1925.
64. T.R. Bieler, J.D. Whittenberger, and M.J. Luton, High-Temperature Ordered Intermetallic Alloys V, Mat. Res. Soc. Symp. Proc. Vol. 288 (Pittsburgh, PA: MRS, 1993), p. 1149.
65. M. Suzuki, S.R. Nutt, and R.M. Aikin, Jr., Intermetallic Matrix Composites II, MRS Symp. Proc., 273, ed. D.B. Miracle, D.L. Anton, and J.A. Graves (Pittsburgh, PA: MRS, 1992), p. 267.
66. M. Suzuki, S.R. Nutt, and R.M. Aikin, Jr., Mater. Sci. Eng., 162 (1993), p. 73.
For more information, contact R.M. Aikin, Jr., Department of Materials Science and Engineering, Case Western Reserve University, 10900 Euclid Avenue, Cleveland, Ohio 44106; telephone (216) 368-4221; fax (216) 368-3209; e-mail: rxa19@po.cwru.edu.
Direct questions about this or any other JOM page to jom@tms.org.
| Search | TMS Document Center | Subscriptions | Other Hypertext Articles | JOM | TMS OnLine |
|---|